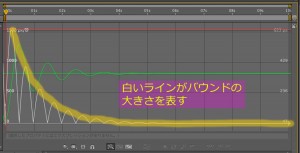
前回に続いて、今のところ、ここまでできた。

var amplitude=100;
var x=transform.position[0];
var y=transform.position[1]-(amplitude*Math.cos(time));
[x,y]

バウンドの大きさを大きくします。

var amplitude=300;
var x=transform.position[0];
var y=transform.position[1]-(amplitude*Math.cos(time));
[x,y]

変数frequencyを使って、バウンドの回数をコントロールします。
数値が大きいほうがたくさんバウンドします。

var amplitude=300;
var frequency=1;
var x=transform.position[0];
var y=transform.position[1]-(amplitude*Math.cos(frequency*time));
[x,y]

ココまでできたところで、グラフエディタを見てみると、こうなってます。

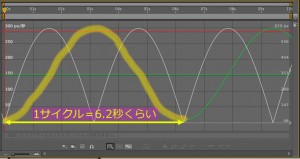
一応周期的に動いているものの、その周期が6秒ちょっと。
これを切りのいい1秒にします。

var amplitude=300;
var frequency=1;
var x=transform.position[0];
var y=transform.position[1]-
(amplitude*Math.cos(frequency*time*2*Math.PI));
[x,y]

2*Math.PIというのは、「2×3.1415…」のこと。
frequency*time*2*Math.PIは1秒あたりのバウンド回数を決めます。

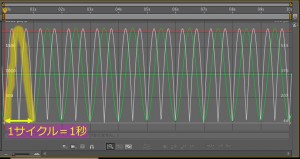
どうしてそうなるかについては、角度（degree）とラジアン（radian）の関係を知らないといけないのですが、それを理解するだけでひと仕事なもので、省略。

とりあえず分からなくても、frequency*time*2*Math.PIが1秒あたりの回数を決めるって丸覚えしておけばいいんだよ、とエクスプレッションの教則本にも書いてました。
これで、バウンドの大きさ/回数/周期はできました。

でも、プレビューすると分かりますが、いつまでたっても同じ勢いでバウンドし続けています。
これを時間が経つに連れて、バウンドが小さくなるようにします。
そこでMath.expで割り算して（’/’＝スラッシュは割り算のこと）、バウンドを徐々に小さくします。

var amplitude=300;
var frequency=1;
var x=transform.position[0];
var y=transform.position[1]-
(amplitude*Math.cos(frequency*time*2*Math.PI)/Math.exp(time));
[x,y]

どうなったかグラフエディタで見てみると…

バウンドの大きさをオレンジ色の太線でなぞってますが、急激に小さくなってます。
この変化をコントロールするために、さらにdecayという変数を使います。

var amplitude=300;
var frequency=1;
var decay=0.5;
var x=transform.position[0];
var y=transform.position[1]-
(amplitude*Math.cos(frequency*time*2*Math.PI)/Math.exp(decay*time));
[x,y]

decay=1だと、何も変わりません。
数値を大きくすると、より急激に変化し、数値を小さくすると緩やかに変化します。
ここでは、ゆっくりとバウンドを鎮めたいので0.5にしてみました。
グラフエディタであらためて見てみると、こうなります↓

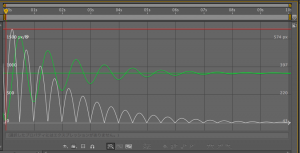
/Math.exp(time)だけに比べて、バウンドが長持ちしていますね。
さて、仕上げです。

今のボールのバウンドは、落下地点のピクセル（高さ）が一定していません。
Math.cosの「1→0→-1→0→1」という周期的変化を基にしているので、仕方ないのですが。

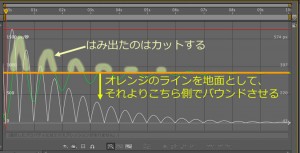
この問題は、Math.absを使うことで解決します。
abs=absolute value（絶対値）からきてますので、なんとなく役割がイメージできますね。

var amplitude=300;
var frequency=1;
var decay=0.5;
var x=transform.position[0];
var y=transform.position[1]-
[amplitude*Math.abs(Math.cos(frequency*time*2*Math.PI)
/Math.exp(decay*time))];
[x,y]

丸括弧を角括弧に変えたのは、最後に丸括弧が3つ続いて、ややこしかったから。
別に丸括弧のままでも支障はなかったです。

いちおう、角括弧のほうが丸括弧より優先度が高いはずだったので、変えてみました。
これで、グラフエディタを確認してみますと↓

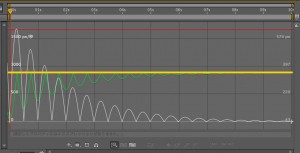
スパッとオレンジライン（地面）から下（ピクセル数が大きい側）が消えてます。
正確には反転したんですけど。
これでボールのバウンドが完成しました。

実際のモーションは過去記事にあるのでそっちでどうぞ。
長々と書き連ねましたが、これでおしまい。

Tweet